Números reales – Matemáticas I
18 sep
Aqui les comparto esta informacion de matematicas I, el tema es numeros reales
Agradecemos tus comentarios y sugerencias para mejorar nuestra pagina 
Números reales
Para poder explicar y entender el tema de los números reales utilizaremos los diagramas de Venn.
Diagrama de los numeros reales
Observando y analizando este diagrama podemos concluir que:
- Los números reales están contenidos en los números complejos.
- Los números reales se forman por la unión de los números racionales e irracionales.
- Los números racionales contienen a los números enteros y números naturales.
Mapa conceptual de los números reales.
NUMEROS FRACCIONARIOS
Números Fraccionarios
Propiedades Generales
Debido a mediciones u operaciones como la medición de las cantidades continuas o las divisiones inexactas, los números fraccionarios se han vuelto más importantes y necesarios en las matemáticas y la vida diaria.
NÚMERO FRACCIONARIO O QUEBRADO
Comúnmente conocido como fracción, el quebrado o número fraccionario es el que expresa 1 o más partes iguales de la unidad central. Según la cantidad en la que se divide la unidad, ésta va cambiando de nombre. Por ejemplo si está dividida en 2 se le llama medios, en 3 tercios, 4 cuartos, 5 quintos, 6 sextos, 7 séptimos, 8 octavos, 9 novenos, 10 décimos, etc…
Sus términos
La fracción está compuesta por 2 términos básicos, el numerador y el denominador.
El numerador menciona en cuantas partes se ha dividido la unidad, mientras el denominador indica cuantas partes se toman de la unidad.
Por ejemplo:
Su escritura
Una fracción tiene 2 formas de escribirse (notación). La primera es colocando una línea horizontal entre el numerador y el denominador. Por ejemplo:
La otra forma es colocando una línea diagonal entre ambos números. Por ejemplo:
9 / 5, 3 / 6, 10 / 8
Lectura
La forma para leer un quebrado es muy sencilla: primero se lee el numerador tal y como decimos comúnmente los números: un, dos, tres, cuatro, etc…
Con respecto al denominador lo leemos así: 2 es medios, 3 es tercios, 4 cuartos, 5 quintos, 6 sextos, 7 séptimos, 8 octavos, 9 novenos y 10 décimos.
En caso que el numerador sea mayor que 10, se le añade al número la terminación -avo. Con esa regla, podríamos decir que 11 se lee onceavo, 12 doceavo, 13 treceavo, etc...
Por ejemplo:
8 / 5 se lee ocho quintos
10 / 35 se lee diez treintaicincoavos
1
Clases
Podríamos decir que las fracciones se dividen en 2 tipos:
- Fracción Común: es la fracción cuyo denominador no es la unidad seguida de ceros. Por ejemplo:
- Fracción Decimal: es la fracción que tiene como denominador la unidad seguida de ceros. Por ejemplo:
Tipos
Toda fracción, sin importar que sea decimal o común, pueden ser fracciones:
- Propias: son las fracciones que tienen el numerador menor que el denominador. Por ejemplo:
- Impropias: son las fracciones que tienen el numerador mayor que el denominador. Por ejemplo:
- Unitarias: son las que tienen el mismo numerador y denominador. Por ejemplo:
- Número Mixto: una fracción mixta es aquella que contiene un número entero y una fracción. Por ejemplo:
Algunas afirmaciones que podemos hacer con respecto a las fracciones son:
- Toda fracción propia es menor que la unidad.
- Toda fracción impropia es mayor que la unidad,
- Toda fracción unitaria es igual a la unidad
- Toda número mixto contiene un número exacto de unidades y además una o varias partes iguales a la unidad.
- De varias fracciones que tengan igual denominador es mayor la que tenga mayor denominador
- De varias fracciones que tengan el mismo numerador es mayor la que tenga menor denominador
- Si a los 2 términos de una fracción propia (numerador y denominador) se les suma un mismo número, la fracción nueva es mayor que la primera
- Si el numerador o el denominador de una fracción es multiplicado por cierto número, la nueva fracción queda multiplicada por dicho número y en caso que se divida, queda dividida.
- Si los 2 términos de una fracción se multiplican o dividen por un mismo número, la fracción no varía
- Si a los 2 términos de una fracción propia se le resta un mismo número, la nueva fracción es menor que la primera.
- Si a los 2 términos de una fracción impropia se les suma un mismo número, la fracción nueva es menor que la anterior, sin embargo si se les resta un mismo número la nueva fracción va a ser mayor que su antecesora.
¿Cómo convierto un número mixto en fracción impropia?
- Muy sencillo, se multiplica el entero por el denominador y el producto se le suma al numerador. El denominador es el mismo. Por ejemplo:
6 ½
En ese caso, se realiza la operación: 6 x 2 + 1. Así quedaría la fracción 13 / 2.
¿Cómo sé cuantos enteros hay en una fracción impropia?
- Se divide el numerador por el denominador. Si el cociente es exacto, el mismo representa los enteros, pero si la división es inexacta, el residuo es el numerador y el divisor es el denominador. Por ejemplo:
9 / 5 = 9: 5 = 4 (número entero)
¿Cómo reduzco un número entero a fracción?
- Existen 2 formas:
3 = 3 / 1, 24 = 24 / 1
Cuando se nos da un denominador específico, lo que se hace es multiplicar ese número por el denominador dado, de ese modo sacamos el numerador. El denominador es el que nos dieron. Por ejemplo:
Número entero = 13
Denominador dado = 5
13 x 5 = 65
Fracción = 65 / 5
3
- Para multiplicar una fracción lo único que se hace es multiplicar el numerador y denominador por el número dado o deseado. Por ejemplo:
3 / 9
3 x 3 = 9
9 x 3 = 27
Nueva fracción: 9 / 27
- Para reducir una fracción se divide el numerador y el denominador entre un número que pueda dividir a ambos de forma exacta. Por ejemplo:
24 / 12
24 : 2 = 12
12 : 2 = 6
Nueva fracción: 12 / 6
- Es la fracción que, como su nombre lo dice, no se puede reducir más utilizando factores primos. Esto ocurre porque el numerador y el de-
7 / 5, 20 / 33
¿A qué se refiere el término “simplificación de fracciones”?
- Esta expresión se refiere a convertir una fracción en otra equivalente cuyos términos (denominador y numerador) sean menores. Para eso se dividen sus 2 términos sucesivamente por los factores comunes que tengan. Por ejemplo:
LOS NUMEROS DECIMALES
Se denominan números decimales aquellos que poseen una parte decimal, en oposición a los números enteros que carecen de ella.[1] Así, un número x perteneciente a R escrito usando la representación decimal tiene la siguiente expresión:

- El punto decimal: se emplea un punto(.) para separar la parte entera de la decimal, este método es el utilizado en las calculadoras electrónicas y en los ordenadores, rara vez se utiliza en la notación de cifras manualmente.
Cifras decimales

Cuando dices "por ciento" en realidad dices "por cada 100"
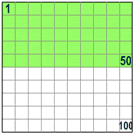 | Así que 50% quiere decir 50 por 100 (50% de la caja es verde) | 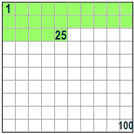 |
| Y 25% quiere decir 25 por 100 (25% de la caja es verde) |
Ejemplos: Porcentajes de 80
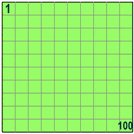 | 100% of 80 is 100/100 × 80 = 80 So 100% means all. |
 | 50% of 80 is 50/100 × 80 = 40 So 50% means half. |
 | 5% of 80 is 5/100 × 80 = 4 So 5% means 5/100ths. |
Usando porcentajesComo "por ciento" quiere decir "por cada 100" deberías pensar siempre que "hay que dividir por 100"Así que 75% quiere decir 75/100 Y 100% es 100/100, o exactamente 1 (100% de cualquier número es el mismo número) Y 200% es 200/100, o exactamente 2 (200% de cualquier número es el doble del número) Usa la barra de la izquierda y experimenta un poco (por ejemplo, ¿cuánto es el 60% de 80?) |
Un porcentaje también se puede escribir como un decimal o una fracción
 |
| ||||||||||
Algunos ejemplos detallados
Calcula 25% de 80 | ||
| 25% = 25/100 | (25/100) × 80 = 20 | |
Así que 25% de 80 es 20 | ||
Un Skateboard tiene una rebaja de 25%. El precio normal es $120. Calcula el nuevo precio | ||
Calcula 25% de $120 | ||
| 25% = 25/100 | (25/100) × $120 = $30 | |
25% de $120 es $30 | ||
Así que la reducción es $30 | ||
| Quita la reducción del precio original | $120 - $30 = $90 | |
Término general de una progresión aritmética
El término general de una progresión aritmética es aquel en el que se obtiene cualquier término restándole la diferencia al término siguiente. El término de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión. La fórmula del término general de una progresión aritmética es:Donde d es un número real llamado diferencia. Si el término inicial de una progresión aritmética es
 y la diferencia común es
y la diferencia común es  , entonces el término
, entonces el término  -ésimo de la sucesión viene dada por
-ésimo de la sucesión viene dada por , n = 0, 1, 2,... si el término inicial se toma como el cero.
, n = 0, 1, 2,... si el término inicial se toma como el cero.
 n = 1, 2, 3,... si el término inicial se toma como el primero.
n = 1, 2, 3,... si el término inicial se toma como el primero.
La primera opción ofrece una fórmula más sencilla, ya que es común en el lenguaje el uso de "cero" como ordinal. Generalizando, sea la progresión aritmética:
tenemos que:de diferencia
sumando miembro a miembro todas esas igualdades, y simplificando términos semejantes, obtenemos:
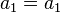
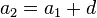

- ...


expresión del término general de la progresión, conocidos su primer término y la diferencia. Pero también podemos escribir el término general de otra forma. Para ello consideremos los términos(I)
 y
y  (
( ) de la progresión anterior y pongámolos en función de
) de la progresión anterior y pongámolos en función de  :
:Restando ambas igualdades, y trasponiendo, obtenemos:

expresión más general que (I) pues nos da los términos de la progresión conociendo uno cualquiera de ellos, y la diferencia.(II)
Dependiendo de que la diferencia
 de una progresión aritmética sea positiva, nula o negativa, tendremos:
de una progresión aritmética sea positiva, nula o negativa, tendremos:- d>0: progresión creciente. Cada término es mayor que el anterior.
- Ejemplo: 3, 6, 9, 12, 15, 18... (
 )
)
- Ejemplo: 3, 6, 9, 12, 15, 18... (
- d=0: progresión constante. Todos los términos son iguales.
- Ejemplo: 2, 2, 2, 2, 2... (
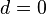 )
)
- Ejemplo: 2, 2, 2, 2, 2... (
- d<0: progresión decreciente. Cada término es menor que el anterior.
- Ejemplo: 5, 3, 1, -1, -3, -5, -7... (
 )
)
- Ejemplo: 5, 3, 1, -1, -3, -5, -7... (
Una progresión geométrica está constituida por una secuencia de elementos en la que cada uno de ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de la progresión. Se suele reservar el término progresión cuando la secuencia tiene una cantidad finita de términos mientras que se usa sucesión cuando hay una cantidad infinita de términos, si bien, esta distinción no es estricta.
Así,
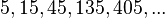 es una progresión geométrica con razón igual a 3, porque:
es una progresión geométrica con razón igual a 3, porque:- 15 = 5 × 3
- 45 = 15 × 3
- 135 = 45 × 3
- 405 = 135 × 3
- 1215 = 405 × 3
- 3645 = 1215 × 3
- 45 = 15 × 3
Aunque es más fácil aplicando la fórmula:
Siendo
 el término en cuestión,
el término en cuestión,  el primer término y
el primer término y  la razón:
la razón:Así quedaría si queremos saber el 6º término de nuestra progresión








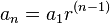
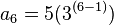
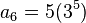
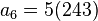
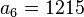
No hay comentarios:
Publicar un comentario